Pythagoras sats

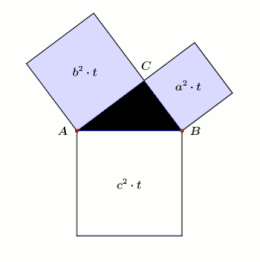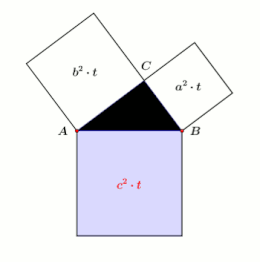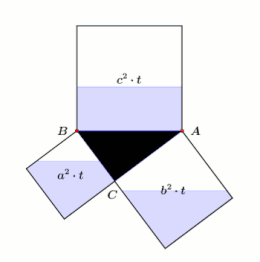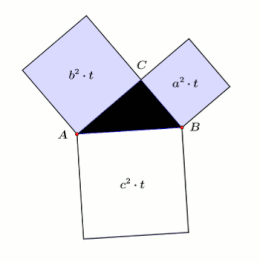
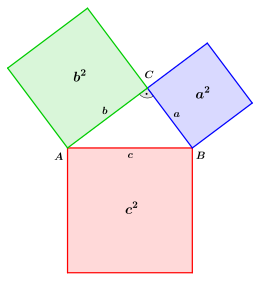
Den pythagoreiska satsen (även hypotenus ) är en av de grundläggande satserna för den euklidiska geometrin . Det står att i alla plana högra trianglar är summan av ytorna på cathetus-kvadraterna lika med området för hypotenus-kvadraten. Om och är de längder av de sidor angränsande den räta vinkeln , den katetem , och längden på den sida som är motsatt den räta vinkeln, den hypotenusan , då satsen är uttryckt som en ekvation : ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c}$

${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$

Satsen är uppkallad efter Pythagoras från Samos , som sägs ha varit den första som hittade ett matematiskt bevis för det, vilket emellertid är kontroversiellt i forskning. Satsen om satsen var känd i Babylon och Indien långt före Pythagoras tid , men det finns inga bevis för att bevis också fanns där.

Matematiskt uttalande

Satsen för Pythagoras kan formuleras enligt följande:

Om , och är sidolängder av en rätvinklig triangel, där och är längderna hos katetem och längden på hypotenusan, tillämpar sedan .${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c}$${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$

I en geometrisk tolkning, i en rätt triangel, är summan av ytorna på de två kvadraterna ovanför katetus lika med kvadratytan ovanför hypotenusen.

Baksidan av meningen gäller också:

Om ekvationen i en triangel med sidlängderna , och , är den här triangeln rätvinklad med rätt vinkel mot sidan .${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c}$${\ displaystyle c}$

Nära släkt med Pythagoras sats är höjdsatsen och katetuslagen . Dessa två meningar och Pythagoras teorem bildar tillsammans den Pythagoras meningsgrupp . Den kosinosats som beskrivs nedan är en generalisering av den pythagoreiska satsen.

använda sig av

Längder i rätt triangel

Från Pythagoras sats följer det direkt att längden på hypotenusen är lika med kvadratroten av summan av cathetus- kvadraterna , d.v.s.

${\ displaystyle c = {\ sqrt {a ^ {2} + b ^ {2}}}}$.

En enkel och viktig tillämpning av satsen är att beräkna den tredje från två kända sidor av en rätt triangel. Detta är möjligt genom att omvandla ekvationen för alla sidor:

${\ displaystyle {\ begin {align} a & = {\ sqrt {c ^ {2} -b ^ {2}}} \\ b & = {\ sqrt {c ^ {2} -a ^ {2}} } \ end {align}}}$

Teoremets baksida kan användas för att kontrollera att en given triangel är rätvinklad. För detta ändamål testas det om teoremens ekvation gäller sidorna av den givna triangeln. Att veta längden på sidorna av en viss triangel är tillräckligt för att avgöra om den är rätvinklad eller inte:

• Är sidlängderna z. B. , och därefter resultat , och därför är triangeln rektangulär.${\ displaystyle 3}$${\ displaystyle 4}$${\ displaystyle 5}$${\ displaystyle 3 ^ {2} + 4 ^ {2} = 9 + 16 = 25 = 5 ^ {2}}$
• Är sidlängderna z. B. , och därefter resultat , och därför är triangeln inte rät vinklad.${\ displaystyle 4}$${\ displaystyle 5}$${\ displaystyle 6}$${\ displaystyle 4 ^ {2} + 5 ^ {2} = 16 + 25 = 41 \ neq 6 ^ {2}}$

Av Pythagoras sats följer att hypotenusen i en rätt triangel är längre än var och en av kateterna och kortare än deras summa. Det senare är också resultatet av ojämlikheten i triangeln .

Pythagoras tripplar

Av alla tripplar som uppfyller ekvationen , det finns oändligt många där , och är vardera heltal . Dessa grupper om tre kallas Pythagoras tripplar. Den enklaste av dessa tripplar består av siffrorna , och . Pythagoras tripplar har använts för konstruktion av rätt trianglar sedan urminnes tider. Ett exempel är den tolvknutiga linan som används för att lägga en triangel vars sidor har längderna , och . De två kortsidorna bildar sedan en rät vinkel. ${\ displaystyle (a, b, c)}$${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c}$${\ displaystyle 3}$${\ displaystyle 4}$${\ displaystyle 5}$${\ displaystyle 3}$${\ displaystyle 4}$${\ displaystyle 5}$

Den stora Fermatsche-satsen hävdar att ett tal, om det är, inte kan representeras som summan av två krafter i samma grad. Vad menas är hela bastal och naturliga exponenter. Generellt sett betyder detta: ${\ displaystyle n}$${\ displaystyle n> 2}$${\ displaystyle \ neq 0}$

Ekvationen har ingen lösning för heltal och naturliga tal .${\ displaystyle a ^ {n} + b ^ {n} = c ^ {n}}$ ${\ displaystyle a, b, c \ neq 0}$ ${\ displaystyle n> 2}$

Det här är fantastiskt eftersom det finns ett oändligt antal lösningar för. För dessa är de pythagoriska tripletterna. ${\ displaystyle n \ leq 2}$${\ displaystyle n = 2}$

Euklidiskt avstånd

Pythagorasatsningen ger en formel för avståndet mellan två punkter i ett kartesiskt koordinatsystem . Om två punkter och ges i ett plan , är deras avstånd genom ${\ displaystyle (x_ {0}, y_ {0})}$${\ displaystyle (x_ {1}, y_ {1})}$${\ displaystyle c}$

${\ displaystyle c = {\ sqrt {(x_ {1} -x_ {0}) ^ {2} + (y_ {1} -y_ {0}) ^ {2}}}}$

given. Detta utnyttjar det faktum att koordinataxlarna är vinkelräta mot varandra. Denna formel kan också utökas till mer än två dimensioner och ger sedan det euklidiska avståndet . Till exempel i tredimensionellt euklidiskt utrymme

${\ displaystyle c = {\ sqrt {(x_ {1} -x_ {0}) ^ {2} + (y_ {1} -y_ {0}) ^ {2} + (z_ {1} -z_ {0 }) ^ {2}}}}$.

bevis

Flera hundra bevis är kända för satsen, vilket gör den till den mest beprövade matematiska satsen. Som ett exempel presenteras fem geometriska bevis nedan. Ett sjätte bevis från år 1875 av James A. Garfield kan hittas under beviset från Garfields Pythagorasats , vilket mycket liknar beviset genom komplettering .

Bevis genom att lägga till härledda områden

Beviset, illustrerat på olika sätt i de två intilliggande bilderna genom att lägga till härledda områden , kommer från det kinesiska verket Zhoubi suanjing , översatt klassisk aritmetik av Gnomon och himmelens cirklar (man antar nu att verket ”går tillbaka till slutet av 4-talet tidigast f.Kr. "). Det är här den välkända rätvinklig triangel med sidorna och används. ${\ displaystyle 3, \; 4}$${\ displaystyle 5}$

Efter dragning av en kvadrat (Figur 1) och dess indelning i x enhet torg, den rektangulära utgångs triangeln (röd) med kortsidorna , och med den resulterande hypotenusan in med hjälp av gittret. Dessutom placeras tre trianglar som är identiska med starttriangeln på ett sådant sätt att hypotenuserna resulterar i en inre kvadrat och därmed avgränsar en central enhets kvadrat (gul) med området . Ett rutnät ritat på den inre kvadraten, som liknar den yttre och omsluter en rät vinkel med hypotenusen , ger x enhetskvadrater. ${\ displaystyle 7}$${\ displaystyle 7 = 49}$${\ displaystyle a = 3}$${\ displaystyle b = 4}$${\ displaystyle c}$${\ displaystyle = 1 ^ {2}}$${\ displaystyle 5}$${\ displaystyle 5 = 25}$

Arean på det inre torget med de fyra trianglarna och centralenhetens kvadrat motsvarar enhets kvadrater . Det totala antalet (gula) enhetsrutor är resultatet av enhetsrutorna för det yttre torget minus de fyra triangulära områdena för det inre torget; detta ger också enhetsfyrkanter. ${\ displaystyle 4 \ cdot {\ tfrac {3 \ cdot 4} {2}} + 1 = 25}$${\ displaystyle 49}$${\ displaystyle 49-4 \ cdot {\ tfrac {3 \ cdot 4} {2}} = 25}$

Sidolängden på det inre torget är hypotenusen, så det är en allmän formel ${\ displaystyle c,}$

${\ displaystyle c ^ {2} = 4 \ cdot {\ frac {a \ cdot b} {2}} + \ left (ab \ right) ^ {2} = a ^ {2} + b ^ {2}. }$

Värden för och används: ${\ displaystyle a}$${\ displaystyle b}$

${\ displaystyle c ^ {2} = 4 \ cdot {\ frac {3 \ cdot 4} {2}} + \ left (3-4 \ right) ^ {2} = 3 ^ {2} + 4 ^ {2 } = 25 \; [\ mathrm {FE}]}$ (Area enheter) ${\ displaystyle \ Rightarrow}$

${\ displaystyle c = 5 \; [\ mathrm {LE}]}$ (Längdenheter)

Animationen (fig. 2) illustrerar detta på ett jämförbart sätt.

Bevis mot tillägg

Fyra kongruenta rätvinkliga trianglar med sidorna , och (hypotenusan) införs i en kvadrat med sidolängden . Detta kan göras på två sätt som visas i diagrammet. ${\ displaystyle a + b}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c}$

Områdena för vänster och höger kvadrat är lika (sidolängd ). Den vänstra består av de fyra rätvinkliga trianglarna och en fyrkant med sidolängd , den högra med samma trianglar och en fyrkant med sidolängd och en med sidolängd . Området motsvarar summan av området och området , det vill säga ${\ displaystyle a + b}$${\ displaystyle c}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c ^ {2}}$${\ displaystyle a ^ {2}}$${\ displaystyle b ^ {2}}$

${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$.

En algebraisk lösning är resultatet av den vänstra bilden i diagrammet. Det stora torget har sidolängden och därmed området . Om du subtraherar de fyra trianglarna från detta område, som var och en har ett område på (dvs. totalt ), förblir området kvar. Så är det ${\ displaystyle a + b}$${\ displaystyle (a + b) ^ {2}}$${\ displaystyle {\ tfrac {from} {2}}}$${\ displaystyle 2ab}$${\ displaystyle c ^ {2}}$

${\ displaystyle (a + b) ^ {2} = 2ab + c ^ {2}}$.

Lösa upp fästanordningarna

${\ displaystyle a ^ {2} + 2ab + b ^ {2} = 2ab + c ^ {2}}$.

Om du nu subtraherar på båda sidor förblir den Pythagoras satsen. ${\ displaystyle 2ab}$

Skjuvsäker

En möjlighet är att skjuva katetusfyrkantarna i hypotenus-torget. I geometri förstås skjuvningen av en rektangel som omvandlingen av rektangeln till ett parallellogram samtidigt som höjden bibehålls. Under skjuvningen har det resulterande parallellogrammet samma område som startrektangeln. De två mindre kvadraterna kan sedan omvandlas till två rektanglar, som tillsammans passar exakt in i det stora torget.

När det gäller ett exakt bevis måste det sedan demonstreras via kongruenssatserna i triangeln att den mindre sidan av de resulterande rektanglarna motsvarar den relevanta hypotenusavsnittet. Som vanligt anges i animeringen höjden med och hypotenus-segmenten med . ${\ displaystyle h}$${\ displaystyle p, q}$

Bevis med likheter

Det är inte absolut nödvändigt att använda (uttryckligen) ytor för att bevisa Pythagoras sats. Det är geometriskt mer elegant att använda likheter. Så snart du har övertygat dig genom att beräkna vinkelsummor i triangeln att de två vinklar i bilden nedan måste vara densamma, kan man se att trianglar , och är likartade. Beviset för Pythagoras-teorem resulterar sedan som visas på bilden, man bevisar också cathetus-satsen och tillsatsen av båda varianterna av kateterteoremet resulterar i att Pythagoras själva förklaras. Eftersom deras yta är proportionell mot området för de intilliggande rutorna representerar ekvationen ${\ displaystyle \ delta}$${\ displaystyle ABC}$${\ displaystyle BCD}$${\ displaystyle ADC}$

${\ displaystyle ADC + BCD = ABC}$

meningen.

Bevis på vändningen

Teoremets inversion kan bevisas på olika sätt, men ett särskilt enkelt bevis erhålls om man använder den Pythagoras teorem själv för att bevisa sin inversion.

För varje triangel vars sidor uppfyller villkoret , konstruera en andra triangel. Detta har en rät vinkel, vars benlängder motsvarar sidolängderna på och . Enligt Pythagoras teorem är längden på hypotenusen i denna andra triangel nu längden på sidan av starttriangeln . De två trianglarna har därför samma sidlängder och är kongruenta på grund av den första kongruenssatsen (SSS). Detta innebär att deras vinklar då också är desamma, det vill säga starttriangeln har också en rät vinkel som är mittemot sidan . ${\ displaystyle a, b, c}$${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2}}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle {\ sqrt {a ^ {2} + b ^ {2}}}}$${\ displaystyle c}$${\ displaystyle c}$

Generaliseringar och avgränsning

Cosinus lag

Den cosinus lagen är en generalisering av Pythagoras sats för varje triangel:

${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab \ cdot \ cos \ gamma}$,

där vinkeln mellan sidorna är och . Cosinuslagen skiljer sig sålunda från den pythagoreiska satsen med termen . Eftersom cosinus av noll är, faller denna term i rät vinkel bort, och det finns ett speciellt fall av Pythagoras teorem. Omvänt, om förhållandet gäller i en triangel ${\ displaystyle \ gamma}$${\ displaystyle a}$${\ displaystyle b}$ ${\ displaystyle -2ab \ cdot \ cos \ gamma}$${\ displaystyle 90 ^ {\ circ}}$

${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2}}$,

så måste det vara, från vilket det följer, och därmed är triangeln rätvinklig. Den Detsamma gäller akuta trianglar${\ displaystyle -2ab \ cdot \ cos \ gamma = 0}$${\ displaystyle \ gamma = 90 ^ {\ circ}}$

${\ displaystyle c ^ {2} <a ^ {2} + b ^ {2}}$

och för trubbiga trianglar

${\ displaystyle c ^ {2}> a ^ {2} + b ^ {2}}$.

Generalisering av Thabit ibn Qurra

En generalisering som går tillbaka till Thabit ibn Qurra ger kvadraterna över två sidor av vilken triangel som helst, en rektangel över den tredje sidan, vars yta motsvarar summan av de två kvadratiska områdena.

För varje triangel med sidor , vinklar på och höjd konstruerar du en likbent triangel vars bas är på sidan och som har höjden. Dessutom har de två basvinklarna samma storlek som när det är en spetsig vinkel. Om däremot en tråkig vinkel, bör basvinklarna vara. Vidare betecknas hörnpunkten för den likbeniga triangeln, som ligger på samma sida av som, med E och den andra hörnpunkten på samma sida som med . Detta gäller dock bara i fallet , för istället bytte till och . I fallet sammanfaller den likbeniga triangeln med höjden och punkterna och följaktligen med punkten . Om man definierar och gäller följande: ${\ displaystyle \ triangel ABC}$${\ displaystyle a, b, c}$${\ displaystyle \ gamma}$${\ displaystyle C}$${\ displaystyle CD}$${\ displaystyle CFE}$${\ displaystyle c}$${\ displaystyle CD}$${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$${\ displaystyle 180 ^ {\ circ} - \ gamma}$${\ displaystyle CD}$${\ displaystyle B}$${\ displaystyle A}$${\ displaystyle F}$${\ displaystyle \ gamma <90 ^ {\ circ}}$${\ displaystyle \ gamma> 90 ^ {\ circ}}$${\ displaystyle E}$${\ displaystyle F}$${\ displaystyle \ gamma = 90 ^ {\ circ}}$${\ displaystyle CD}$${\ displaystyle E}$${\ displaystyle F}$${\ displaystyle D}$${\ displaystyle r = | AE |}$${\ displaystyle s = | BF |}$

${\ displaystyle c (r + s) = a ^ {2} + b ^ {2}}$

För gäller här och ovanstående ekvation levererar den pythagoreiska satsen. ${\ displaystyle \ gamma = 90 ^ {\ circ}}$${\ displaystyle c = r + s}$

Analogt med Pythagoras sats, kan uttalandet bevisas direkt med liknande trianglar, där trianglarna , och är likartade.${\ displaystyle \ triangel ABC}$${\ displaystyle \ triangel AEC}$${\ displaystyle \ triangel FBC}$

På grund av

${\ displaystyle 2ab \ cos (\ gamma) = a ^ {2} + b ^ {2} -c ^ {2} = c (r + s) -c ^ {2} = c (r + sc)}$

Qurras generalisering ger också en geometrisk representation av korrigeringsuttrycket i cosinuslagen som en rektangel adderad till eller subtraherad från kvadraten ovanför sidan för att ge ett område som är lika med summan av arean av rutorna ovanför sidorna och . ${\ displaystyle c}$${\ displaystyle a}$${\ displaystyle b}$

Ansiktsuppsättning av pappus

Områdesformeln för Pappus ger en ytterligare generalisering till godtyckliga trianglar . Här, från två parallellogram över två sidor av vilken triangel som helst, blir ett tydligt definierat parallellogram över den tredje sidan av triangeln, vars yta motsvarar summan av ytorna för de två inledande parallellogramen. Om de två inledande parallellogrammen är kvadrater, i fallet med en rätvinklig triangel erhålls en kvadrat över tredje sidan och därmed Pythagoras sats.

Parallellogrammet över den tredje sidan erhålls genom att förlänga de två sidorna av startparallellogrammen som är parallella med sidorna av triangeln och ansluta deras skärningspunkt med triangelns hörnpunkt, som också finns på båda parallellogramen. Denna anslutningslinje ger det andra paret av sidorna av parallellogrammet över den tredje sidan (se ritning).

Liknande figurer uppförda över sidorna av den högra triangeln

En generalisering av Pythagoras sats med hjälp av tre liknande figurer ovanför triangelns sidor (förutom de redan kända rutorna ) infördes redan av Hippokrates av Chios under 500-talet f.Kr. Är känd och troligen två hundra år senare lade Euclid till element i sitt arbete :

Om man tar upp en figur som liknar de andra två över de tre sidorna och den ursprungliga triangeln (Fig. 1) med ytorna och sedan på grund av deras likhet: ${\ displaystyle a, \; b}$${\ displaystyle c}$${\ displaystyle A, \; B}$${\ displaystyle C,}$

${\ displaystyle {\ frac {A} {a ^ {2}}} = {\ frac {B} {b ^ {2}}} = {\ frac {C} {c ^ {2}}}}$

Om du lägger och i formuläret ${\ displaystyle A}$${\ displaystyle B}$

${\ displaystyle A = {\ frac {C \ cdot a ^ {2}} {c ^ {2}}}, \ B = {\ frac {C \ cdot b ^ {2}} {c ^ {2}} }}$

vi får för summan:

${\ displaystyle A + B = {\ frac {a ^ {2}} {c ^ {2}}} \ cdot C + {\ frac {b ^ {2}} {c ^ {2}}} \ cdot C = {\ frac {a ^ {2} + b ^ {2}} {c ^ {2}}} \ cdot C}$

Enligt Pythagoras sats , är för substituerade och sålunda resulterar: ${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$${\ displaystyle c ^ {2}}$${\ displaystyle a ^ {2} + b ^ {2}}$

${\ displaystyle A + B = C}$

Medan Euclids bevis endast är giltigt för konvexa polygoner (polygoner), är satsen också giltig för konkava polygoner och till och med för liknande figurer med böjda gränser, men dessa figurer härrör också från respektive sida av den ursprungliga triangeln. De områden som visas i figur 2 och de kretsar är bildade från sidorna och de femhörningarna . ${\ displaystyle A, \ B}$${\ displaystyle C}$${\ displaystyle a, \ b}$${\ displaystyle c}$

För att göra det tydligt att enbart cirklar eller halvcirklar , dvs. H. utan polygoner över sidorna, kan användas för generalisering, Pythagoras sats utvidgas med antalet cirklar ${\ displaystyle \ pi:}$

Från uppsättningen med rutor

${\ displaystyle c ^ {2} = a ^ {2} + b ^ {2}}$

blir, med motsvarande sidolängder och som radier, en generalisering med cirklar ${\ displaystyle a, \; b}$${\ displaystyle c}$

${\ displaystyle c ^ {2} \ cdot \ pi = a ^ {2} \ cdot \ pi + b ^ {2} \ cdot \ pi}$

eller en generalisering med halvcirklar:

${\ displaystyle {\ frac {1} {2}} \ cdot c ^ {2} \ cdot \ pi = {\ frac {1} {2}} \ cdot \ left (a ^ {2} \ cdot \ pi + b ^ {2} \ cdot \ pi \ höger)}$

Grundidén bakom denna generalisering är att arean för en plan figur är proportionell mot kvadraten för varje linjär dimension, och i synnerhet proportionell mot kvadraten på längden på varje sida.

Scalar produktutrymmen

Om man abstraherar från vanligt euklidiskt utrymme till allmänna skalära produktutrymmen , dvs. vektorutrymmen med en skalärprodukt , gäller följande:

Om två vektorer och är ortogonala till varandra, dvs deras skalärprodukt , då gäller följande på grund av linjäriteten hos den skalära produkten ${\ displaystyle u}$${\ displaystyle v}$${\ displaystyle \ langle u, v \ rangle = 0}$

${\ displaystyle \ | u + v \ | ^ {2} = \ langle u + v, u + v \ rangle = \ langle u, u \ rangle + \ langle u, v \ rangle + \ langle v, u \ rangle + \ langle v, v \ rangle = \ langle u, u \ rangle + \ langle v, v \ rangle = \ | u \ | ^ {2} + \ | v \ | ^ {2}}$,

där betecknar den norm som induceras av den skalära produkten . ${\ displaystyle \ | \ cdot \ |}$

Om man relaterar denna mening igen till det euklidiska rymden, då och stå för katetus och en rätt triangel. står för längden på hypotenusen . ${\ displaystyle u}$${\ displaystyle v}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle \ | u + v \ |}$${\ displaystyle c}$

Denna generalisering av Pythagoras sats kan också hittas i abstrakta matematiska strukturer, såsom oändliga dimensionella funktionsutrymmen. Det motsatta är också sant. Om ekvationen gäller är de två vektorerna ortogonala mot varandra. Förslaget kan generaliseras ytterligare. Om ett ortogonalt system består av parvisa ortogonala vektorer följer det genom upprepad tillämpning av ovanstående argument: ${\ displaystyle \ {u_ {1}, \ dotsc, u_ {n} \}}$${\ displaystyle u_ {k}}$

${\ displaystyle \ left \ | \ sum _ {k = 1} ^ {n} u_ {k} \ right \ | ^ {2} = \ sum _ {k = 1} ^ {n} \ | u_ {k} \ | ^ {2}}$

Motsvarande uttalande gäller till och med oändliga summor om man betraktar en sekvens av vektorer som alla är ortogonala mot varandra. Om serien nu konvergerar , konvergerar den också och följande gäller: ${\ displaystyle (u_ {k})}$ ${\ displaystyle \ textstyle \ sum _ {k = 1} ^ {\ infty} u_ {k}}$${\ displaystyle \ textstyle \ sum _ {k = 1} ^ {\ infty} \ | u_ {k} \ | ^ {2}}$

${\ displaystyle \ left \ | \ sum _ {k = 1} ^ {\ infty} u_ {k} \ right \ | ^ {2} = \ sum _ {k = 1} ^ {\ infty} \ | u_ { k} \ | ^ {2}}$

Beviset för det andra påståendet följer av kontinuiteten i den skalära produkten. En annan generalisering leder till Parsevals ekvation .

Ytterligare generaliseringar

Lårets tvärsats , Stewart- satsen , Ptolemaios teorem och satsen för den brittiska flaggan kan också betraktas som generaliseringar av Pythagoras sats . Den sistnämnda representerar en generalisering både i plan och i rymden. Pythagoras ekvation ingår också i Apollonios-ekvationen .

En rumslig analog är de Guas teorem . Här den rätvinkliga triangeln är ersatt med en rätvinkligt tetraeder och sidolängderna är ersatta med de områden av sidoytorna. Både Pythagoras teorem och De Gua-satsen är speciella fall av en allmän teorem om n-simplexer med ett rätvinkligt hörn .

Skillnader i icke-euklidisk geometri

Icke-euklidiska geometrier är geometrier där axiomet av paralleller inte gäller. Ett exempel på detta är den sfäriska ytans geometri . Där gäller inte Pythagoras sats längre, eftersom den inre vinkelsatsen inte gäller i sådana geometrier , dvs summan av vinklarna i en triangel skiljer sig från 180 °. Ett annat exempel är det " böjda " utrymmet i Albert Einsteins allmänna relativitetsteori .

historia

Babylon och Indien

Redan på en babylonisk kilformstavla , som är daterad till tiden för Hammurabi-dynastin (ca 1829 till ca 1530 f.Kr.), finns det ett geometriskt problem med en lösning där satsen för beräkning av längder (i sexagesimal-systemet ) var Begagnade:

Detta resulterar i:

${\ displaystyle 0; 18 ^ {2} = 0; 30 ^ {2} -0; 24 ^ {2}}$så och vidare .${\ displaystyle a ^ {2} = c ^ {2} -b ^ {2}}$${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}}$

Källorna visar dock inte att babylonierna var intresserade av ett matematiskt bevis .

Cuneiformtabletten Plimpton 322 innehåller också olika Pythagoras tripplar, bland andra ${\ displaystyle 15}$

${\ displaystyle (56,90,106)}$, liksom ,${\ displaystyle (119,120,169)}$${\ displaystyle (12709,13500,18541)}$

vilket föreslår en metod för beräkning av sådana tripplar.

I indiska Sulbasutras ("regler för klippning" eller "guider till mätkonsten"), som dateras från omkring 6: e till 4: e århundradet f.Kr. Några Pythagoras tripplar kan hittas. Dessutom var satsen redan allmänt uttalad och använd där. Hur det var motiverat är inte säkert.

Kina

Frasen var känd som frasen från Gougu (勾股定理) i det antika Kina . I manuset Zhoubi suanjing (”Arithmetic Classic of the Zhou Gnomonic”), som dateras från omkring 1000-talet f.Kr. F.Kr. till 600-talet e.Kr. illustrerar den så kallade hypotenusfiguren (Xian-tu) ett bevis på den teorem som ges där med hjälp av exemplet med den rätvinkliga triangeln (gougu) med sidorna 3, 4 och 5. Det används också i Jiu Zhang Suanshu ("Nio böcker om aritmetisk teknik", 1: a århundradet e.Kr.), det klassiska matematiska arbetet i Kina med en samling av 263 problem, deras lösningar och möjliga lösningar. Liu Hui (3: e århundradet e.Kr.) gav antagligen i sin kommentar till "Nio Books" i det nionde kapitlet ett bevis på nedbrytning.

Den kontroversiella rollen för Pythagoras

Namnet på meningen efter den grekiska filosofen Pythagoras (600-talet f.Kr.) bekräftas endast i sena källor. Därför är frågan om Pythagoras roll mycket kontroversiell i forskning. Olika hypoteser kan övervägas:

• Pythagoras tog över satsen från babylonierna, hans roll var bara som en medlare för orientalisk kunskap till grekerna. Enligt forntida källor åkte han på en resa till Egypten, han sägs till och med ha varit i Babylonia, men trovärdigheten i rapporterna om hans resor är omtvistad.
• Pythagoras upptäckte satsen oberoende av orientalisk matematik och bevisade det för första gången. Denna uppfattning var utbredd i antiken.
• Pythagoras var skyldig sina kunskaper om saken till orientaliska källor, men var den första som hittade bevis på det. I själva verket verkar babylonierna och egyptierna bara ha varit intresserade av tillämpningen av satsen för praktiska ändamål, inte för något generaliserat bevis. Till exempel innehåller den äldsta kända aritmetikboken i världen, den egyptiska aritmetikboken Ahmes (även Papyrus Rhind ) från 1600-talet f.Kr. Chr., Redan komplicerade uppgifter, men det finns ingen generalisering, det är inte definierat och bevisat.
• Pythagoras spelade ingen roll i propositionens historia; först senare kan Pythagoreans ha hittat det första beviset.

Vetenskapshistorikerna Walter Burkert och Leonid Zhmud representerar motsatta positioner . I bästa fall anser Burkert att Pythagoras förmedlar roll. Zhmud tilldelar honom matematiska prestationer såsom beviset på satsen och betonar hans oberoende från orientalisk matematik.

Euclid , som under andra hälften av 400-talet f.Kr. BC, i sitt berömda arbete, samlade in delar av hans tids matematiska kunskaper, erbjöd ett bevis, men kopplade inte satsen till Pythagoras. Det äldsta beviset för att satsen förknippades med Pythagoras är ett epigram av en Apollodorus som möjligen kan identifieras med filosofen Apollodoros av Cyzicus; i detta fall är verserna från andra hälften av 400-talet f.Kr. Texten lyder:

Apollodorus anger inte vilken "berömd" teckning eller figur han menade, men senare författare, inklusive Diogenes Laertios , som citerade de två verserna på 300-talet, antog att det var "Pythagoras sats". Denna tradition, enligt vilken Pythagoras erbjöd ett nötkreatursoffer till en gud i tacksamhet för att ge honom kunskapen, motsäger det faktum, som har lämnats av många forntida källor, att Pythagoras och Pythagoreerna i princip avvisade djuroffer.

Litterär mottagning

Hans Christian Andersen skrev ett bevis på Pythagoras sats i poesi 1831 med titeln Formens evige Magie (Et poetisk Spilfægterie).

illustration

Objekt som beskriver Pythagoras sats med hjälp av vätskor är mycket vanliga. Det animerade schematiska diagrammet mittemot är så att säga framifrån av en roterbar utställning på Phaeno Science Center i Wolfsburg. På sidorna av den centrala högra triangeln fästs platta transparenta behållare med djupet . Deras kvadratiska basarealer är lika med områdena för cathetus-kvadraterna eller hypotenus-kvadraten. Behållarna är därför märkta med , och . Är utställningen i sitt ursprungliga läge ( botten), strömmar in och blått fylls till randen av vatten över hörnen av triangeln och från helt och därmed helt fyllt . Det följer ${\ displaystyle t}$${\ displaystyle a ^ {2} \ cdot t}$${\ displaystyle b ^ {2} \ cdot t}$${\ displaystyle c ^ {2} \ cdot t}$${\ displaystyle c ^ {2} \ cdot t}$${\ displaystyle a ^ {2} \ cdot t}$${\ displaystyle b ^ {2} \ cdot t}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle c ^ {2} \ cdot t}$

${\ displaystyle a ^ {2} \ cdot t + b ^ {2} \ cdot t = c ^ {2} \ cdot t}$,

dividerat med ger det ${\ displaystyle t}$

${\ displaystyle a ^ {2} + b ^ {2} = c ^ {2}.}$

Relaterade ämnen

• Pythagoras tillägg - kvadratroten av summan av kvadraterna med flera värden
• Trigonometriska Pythagoras - överföringen av satsen till de trigonometriska funktionerna sinus och cosinus
• Hippokrates lilla måne

litteratur

• Anna M. Fraedrich: Pythagoras meningsgrupp . Spektrum Akademischer Verlag, Heidelberg 1994, ISBN 3-86025-669-6 .
• Hans Schupp: Elementär geometri. UTB, Stuttgart 1977, ISBN 3-506-99189-2 , s. 114-118.
• Alexander K. Dewdney : Journey into the Inside of Mathematics. Birkhäuser, Berlin 2000, ISBN 3-7643-6189-1 , s. 47-76.
• Eli Maor : The Pythagorean Theorem: A 4000-year History. Princeton University Press, Princeton 2007, ISBN 0-691-12526-0 .
• Alfred S. Posamentier: The Pythagorean Theorem: The Story of Its Power and Beauty. Prometheus Books, Amherst 2010, ISBN 978-1-61614-181-3 .

webb-länkar

• Stort antal animerade bevis på Pythagoras teorem , statlig utbildningsserver Baden-Württemberg
• Bevis för Pythagoras teorem. ( Memento från den 12 september 2010 i Internetarkivet ). Ordförande för matematikdidaktik, Universitetet i Erlangen-Nürnberg
• Geometrisk bevis för Pythagoras teorem (video)
• Samling av 122 bevis på Pythagoras sats på knutet (engelska)
• Interaktiv handledning med bevis, uppdrag och massor av länkar
• Eric W. Weisstein : Pythagorasats . På: MathWorld (engelska). (Innehåller också olika bevis)

Individuella bevis

1. Hoppa upp ↑ Eli Maor : The Pythagorean Theorem: A 4000-year History. Princeton University Press, Princeton 2007, ISBN 0-691-12526-0 ., P. XIII (förord).
2. ^ Zhou bi, Matematisk Canon av Zhou Gnomonic. Bielefeld University, nås den 24 maj 2019 . 
3. ↑ ^{a b} C.J. Scriba, P. Schreiber: 5000 års geometri - Zhoubi suanjing (Chou Pei Suan Ching) . Red.: H.-W. Alten, A. Djafari Naini, H. Wesemüller-Kock. 3. Upplaga. Springer, Berlin, Heidelberg 2010, ISBN 978-3-642-02361-3 , pp. 111-113 ( springer.com ). 
4. ↑ Michael de Villiers: Thabits generalisering av Pythagoras sats . I: Lärande och undervisning i matematik. Nr 23, 2017, s. 22-23.
5. ↑ Aydin Sayili: Thâbit Ibn Qurras generalisering av Pythagoras teorem. I: Isis. Volym 51, nr 1, 1960, s. 35-37 ( JSTOR ).
6. ↑ George Gheverghese Joseph: The Peacock Crest: Non-European Roots of Mathematics. Princeton University Press, 2011, ISBN 9780691135267 , s.492.
7. ^ Howard Eves: Pappus förlängning av Pythagoras teorem. I: Matematikläraren. Volym 51, nr 7 (november 1958), s. 544-546 ( JSTOR 27955752 ).
8. ^ Claudi Alsina, Roger B. Nelsen: Charmiga bevis: En resa till elegant matematik. MAA, Washington DC 2010, ISBN 978-0-88385-348-1 , s. 77-78 ( begränsad förhandsgranskning i Google Book Search).
9. ^ ^{A b} Thomas Heath: A History of Greek Mathematics, Volym 1,. (a) Hippokrates kvadratur av lunes. I: wilbourhall. Clarendon Press, Oxford, 1921, s. 183 ff., Illustration s. 185 , nås den 25 september 2019 . 
10. ^ Oskar Becker : Antikens matematiska tänkande, Volym 3. Matematik från 500-talet. I: Google Books. Vandenhoeck & Ruprecht, Göttingen, 1966, s.58 , nås den 26 september 2019 . 
11. ↑ ^{a b} Euclid: Stoicheia. Bok VI. (PDF; 529 kB) I: opera-platonis.de/euklid. Hämtad 19 maj 2019 . 
12. ↑ Naber: Pythagorasatsningen en sats om kvadrater? Bielefeld University, nås den 24 maj 2019 . 
13. ↑ London, British Museum , cuneiformtablett 85196 .
14. ↑ Helmuth Gericke : Matematik i antiken och Orienten. Berlin 1984, s. 33 f.
15. ↑ Kurt Vogel : Pre-Greek Mathematics. Del II: Babyloniernas matematik. Hannover / Paderborn 1959, s 67 f.
16. ↑ Kurt Vogel : Pre-Greek Mathematics. Del II: Babyloniernas matematik. Hannover / Paderborn 1959, s. 20.
    Franz Lemmermeyer : Babyloniernas matematik. (PDF; 7,6 MB) 2.4 Det babyloniska mätsystemet. University of Heidelberg, 27 oktober 2015, s.44 ff. , Åtkomst 23 maj 2019 . 
17. ↑ Helmuth Gericke: Matematik i antiken och Orienten. Berlin et al. 1984, sid 66-69.
18. ↑ Oskar Becker: antikens matematiska tänkande. Göttingen 1966, s. 55 f. ( Begränsad förhandsgranskning i Googles boksökning).
19. ↑ Detaljerad förklaring av fakta i Thomas L. Heath: De tretton böckerna om Euclids element. Volym 1. 2: a upplagan, New York 1956, s. 360-364.
20. ↑ Oskar Becker: Grunderna i matematik i historisk utveckling. Freiburg 1964, s. 20.
21. ^ Jean-Claude Martzloff: En historia av kinesisk matematik. Berlin et al. 1997, s. 124, 126.
22. ↑ Helmuth Gericke: Matematik i antiken och Orienten. Berlin 1984, s. 178 f.
23. ^ Jean-Claude Martzloff: En historia av kinesisk matematik. Berlin et al. 1997, s. 298 f.
24. ^ Oskar Becker: antikens matematiska tänkande. Göttingen 1966, s. 56 ( begränsad förhandsvisning i Googles boksökning).
    Helmuth Gericke: Matematik i antiken och Orienten. Berlin 1984, s. 179, å andra sidan, ser inga bevis i detta.
25. ^ Jean-Claude Martzloff: En historia av kinesisk matematik. Berlin et al. 1997, s. 296-298. Tillhörande ritning, som krävs för en korrekt förståelse, har inte bevarats.
26. ^ Walter Burkert: Visdom och vetenskap. Studier av Pythagoras, Philolaus och Platon. Nürnberg 1962, s. 405 f. , 441 ff.
27. ^ Leonid Zhmud: Vetenskap, filosofi och religion i tidig pythagoreanism. Berlin 1997, s. 141–151, 160–163 ( begränsad förhandsvisning i Googles boksökning).
28. ↑ Se även Thomas L. Heath: De tretton böckerna om Euclids element. Volym 1. 2: a upplagan. New York 1956, s. 350-360.
29. ^ Euclid: element. Stoicheia. Bok 1, mening 47 (PDF; 5,6 MB) I: opera-platonis.de. Hämtad 15 juli 2019 . 
30. ↑ Apollodoros efter Diogenes Laertios 8:12, översatt av Otto Apelt : Diogenes Laertios: Berömda filosofers liv och åsikter. 3. Upplaga. Hamburg 1990, s.116.
31. ^ Leonid Zhmud: Pythagoras och de tidiga pythagoreerna. Oxford 2012, s. 59, 257, 267-269.
32. ^ Walter Burkert: Visdom och vetenskap. Studier av Pythagoras, Philolaus och Platon. Nürnberg 1962, s. 168 och anmärkning 152, s. 405 f.
33. ^ Hans Christian Andersen: HC Andersens samlede værker. Volym 7: Digte I. 1823-1839. Köpenhamn 2005, s. 311-313, kommentar s. 638-639 ( visithcandersen.dk ).
34. ↑ Hans-Joachim Schlichting : Världen sett fysiskt. - Former av evig magi. I: hjschlichting.wordpress.com. 9 mars 2017, nås 13 juli 2020 . 
35. ↑ Hans-Joachim Schlichting: Världen sett fysiskt. The Pythagorean Theorem - återbesökt. I: hjschlichting.wordpress.com. 5 mars 2017. Hämtad 11 juli 2019 . 

Denna artikel lades till i listan över utmärkta artiklar den 16 juni 2004 i denna version .