Kontur konstruktion

Kontur: vas med vertikal parallell projektion

sann och tydlig kontur av en sfär med vinkelrät parallell projektion

sann och tydlig kontur av en sfär från en fågelperspektiv (sned parallell projektion)

sann och tydlig form av en sfär i central projektion

I beskrivande geometri används konturerna av dessa områden för att skildra böjda ytor (sfärer, cylindrar, revolutionsytor, ...) . Under konturen kan man föreställa sig ytskurvor som skiljer ytan från dess omgivning för en betraktare (se vänster bild med vasen). Uppenbarligen beror ytans konturer på typen av projektion (vy). Den Följande gäller för släta ytor (det finns ett tangentialplan vid varje punkt): I en kontur punkt en yta, utsprånget strålen är en tangent till ytan. Vid parallell projektion är projektionsriktningen densamma vid varje punkt, med central projektion (strålarna går genom en fast punkt, ögonpunkten) beror projiceringsriktningen på den punkt som ska projiceras. Totaliteten av alla konturpunkter bildar konturen kurvan (eller linjer) av ytan. Till exempel är en sfärs konturkurva i parallell projektion en stor cirkel (cirkelns centrum är också centrum för sfären). Vid central projektion är konturen också en cirkel av sfären, men dess centrum är inte centrum av sfären (se bild). I beskrivande geometri kallas konturkurvan på ytan den sanna konturen . Projektionen av den sanna konturen är en platt kurva (i bilden) och kallas den skenbara konturen . Med en parallell projektion är en sfärs riktiga konturer alltid en stor cirkel. Med vinkelrät parallell projektion är den uppenbara konturen en cirkel som är kongruent till den verkliga konturen (radierna är desamma). Med en fågelperspektiv (sned parallell projektion, se bild) är den synliga konturen en ellips . Vid central projektion är den sanna konturen under alla omständigheter också en cirkel (förutsatt att ögonpunkten ligger utanför sfären). Projiceringen av denna cirkel, d.v.s. den uppenbara konturen, kan vara en cirkel igen, men bara om sfärens centrum är vinkelrätt från ögonpunkten till bildtavlan (se bild). I alla andra fall är den uppenbara konturen av en sfär en ellips när den projiceras från mitten. Ju längre bort sfärens centrum är från den vinkelräta, desto mer förvrängd är den uppenbara konturen.

Som exemplet med vasen visar bidrar inte bara punkter där projektionsriktningen är en tangentriktning till konturen, utan också kantkurvor (lock och bascirkel). Detta måste särskilt beaktas vid beräkningen av konturen. När det gäller ritning gör du detta korrekt "automatiskt".

Du kan få en god uppfattning om den riktiga konturen genom att föreställa dig området som är upplyst med parallellt eller centralt ljus. Den sanna konturen är då självskugggränsen på ytan. Den uppenbara konturen är skugggränsen för området på tavlan.

Som vi visar i avsnittet Beräkna konturen är den sanna konturen inte bara en platt kurva i fallet med en sfär utan i alla kvadrater är den sanna konturen och därmed den uppenbara konturen som en projektion också en konisk sektion ( ellips , hyperbol , parabel , ...). Exemplen på vasen eller torusen (se bild) visar att detta i allmänhet inte är fallet. I allmänhet är beräkningen av konturen ett krävande problem och löses vanligtvis iterat med lämpliga algoritmer. I klassisk beskrivande geometri (med kompass och linjal), för många tekniskt viktiga fall (sfärer, cylindrar, koner, torus, rörytor , ...), kan konturer med vinkelrät parallell projektion bestämmas relativt enkelt med en approximation med en böjd linjal. Nyckeln till denna grafiska approximation ligger i en sfärs enkla kontur: En sfärs kontur är en cirkel med samma radie när den projiceras vinkelrätt parallellt. Konturerna på en yta, som är kuvertet för en grupp sfärer (eventuellt med variabla radier), kan bestämmas grafiskt som kuvertet av cirklar (konturerna av kontakterna) (se avsnitt Ritningsdefinition av konturen ).

När det gäller en polyeder (se bild med oktaeder och ikosaeder) består konturen av en eller flera polygoner (anslutna linjer). Konturen av en polyeder kan lätt bestämmas intuitivt genom att rita. Hur man hittar konturkanterna aritmetiskt förklaras nedan.

Obs: I vissa böcker kallas den sanna konturen också konturen .

Ritningsdefinition av konturen

Konturkonstruktion för cylinder och kon (vertikal parallell projektion)

Kontur av en torus som ett hölje av berörande sfärer (vertikal parallell projektion)

Vas: konturkonstruktion med hjälp av kontaktbollar (vertikal parallell projektion)

Kontur av en singel Hyperboloider som höljet i en familj av raka linjer (vertikal parallell projektion)

Vi börjar från ett område som kan beskrivas som sfärens hölje och vill bestämma konturen för fallet med en vinkelrät parallell projektion i en tvåpanelprojektion (golv och höjd).

Exempel på cylinder

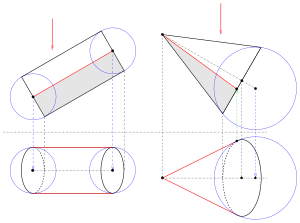
Som ett första exempel väljer vi en cylinder vars axel är parallell med höjdbordet. Höjden visas som en rektangel och är därför lätt att rita. Vi lutar cylinderaxeln så att en tydlig bild framträder i planritningen. Vi betraktar cylindern som höljet för en uppsättning sfärer vars centrum ligger på cylinderaxeln och vars radier är konstant lika med cylinderradien. Eftersom konturen i detta enkla fall består av två parallella linjer är det tillräckligt att titta på två kontaktsfärer (i början och i slutet, se bild). Golvplanerna för sfärernas centrum är lätta att hitta med mappar. Konturerna för dessa sfärer är två cirklar med cylinderns radie. De omslutande raka linjerna ger konturerna. Deras konturer är lika enkla att använda mappar. Delar av basen och locket (elliptiska bågar) visas också som konturer.

Exempel på kon

Så att konens höjd är lätt att rita, väljs konaxeln parallellt med höjdbordet. Konen kan föreställas som kuvert av sfärer med ständigt ökande radier. De raka linjerna går genom konens spets och rör vid kontaktkulan i den nedre cirkeln (se bild). Konturen av denna kontaktboll i planen är återigen en cirkel ("ekvatorcirkel"), vars centrum kan hittas via den tillhörande mappen på planen för konaxeln. Tangenterna till denna kontur av kontakterna (i planen) genom konens spets resulterar i den önskade konturen av konen. Gränserna för konturlinjerna i höjden härrör antingen från mappar från planritningen eller som en sektion av "ekvatorcirkeln" (en linje i höjd) av kontaktsfären med konens nedre cirkel.

Exempel på torus

En torus kan förstås som kuvertet för en uppsättning sfärer med centrum på en cirkel och konstanta radier. Så att höjden av torusen är enkel och planritningen ger en tydlig bild, väljer vi cirkeln av de sfäriska centra vinkelrätt mot höjdbordet och lutas i förhållande till det horisontella (se bild). Konturerna i höjd består av två halvcirkelformade bågar och två parallella linjer (sfärens hölje). Cirkeln av mittpunkterna visas som en ellips i planen. Vi väljer ett tillräckligt antal kontaktfärer genom att välja deras mittpunkter (i planritningen) och rita motsvarande kulkonturer (cirklar i planritningen). Med hjälp av en kurvlinjal eller "frihand" resulterar torusens kontur i planen (röd kurva) som kuvertet för dessa cirklar. Den består av två delar.

Exempel på vas

Vasen (se bild) är en revolutionsyta. Den skapas genom att rotera kurvorna som kan ses i höjden. Så att höjden är så enkel som möjligt väljer vi rotationsaxeln igen parallellt med höjdbordet och lutas till lodrätt. Revolutionens yta kan också förstås som kuvertet för en uppsättning sfärer, kontaktsfärerna, med variabla radier. Om du konstruerar ett tillräckligt antal kontaktbollar (börjar i konturen) och överför deras centrum och konturer till planritningen, blir konturen (i planritningen) som kuvert för tillhörande cirklar. Om konturen i planritningen har ritats ungefär med en böjd linjal kan en konturpunkt markeras för varje touchkula som används i planplanen, som sedan kan överföras till motsvarande "ekvatorialcirkel" för touchkulan i med en mapp. På detta sätt erhålls konturen av konturen (självskugggräns) för vasen.

Exempel på en enkelskalig hyperboloid

En revolution av hyperboloid kan genereras som en yta av revolution genom en lämplig uppsättning kontaktsfärer. Eftersom den enkelskaliga hyperboloid också innehåller raka linjer och täcks av en hel familj av raka linjer, är det också möjligt att här avbilda ett tillräckligt antal linjer vars slutpunkter ligger på botten och toppcirkeln. Kuverten på dessa rader bildar sedan konturen av hyperboloid (se bild).

Matematisk bestämning av konturen

Plansektioner av en sfär

En sfärs plana sektion är antingen tom, består av en punkt eller en cirkel. Detta är lätt att se. Vad du behöver för att beräkna specifika punkter är en parameterrepresentation av korsningscirkeln, om det finns en korsningscirkel (se webblänk CDKG, s. 88).

Givet: Sfär och plan önskat: Parameterrepresentation av skärcirkeln . ${\ displaystyle K: x ^ {2} + y ^ {2} + z ^ {2} = r ^ {2}, \ quad r> 0}$${\ displaystyle \ varepsilon: {\ vec {n}} \ cdot {\ vec {x}} = d}$${\ displaystyle \ varepsilon \ cap K}$

Avståndet från planet till centrum av sfären är . ${\ displaystyle \ varepsilon}$${\ displaystyle \ delta = {\ tfrac {| d |} {\ | {\ vec {n}} \ |}}}$

Om så är fallet är avsnittet tomt .${\ displaystyle \ delta> r}$

Om så är fallet består korsningen av en punkt .${\ displaystyle \ delta = r}$

Om det finns finns det en skärande cirkel .${\ displaystyle \ delta <r}$

a) Korsningscirkelns radie är .${\ displaystyle \ rho = {\ sqrt {r ^ {2} - \ delta ^ {2}}}}$

b) Centret är .${\ displaystyle {\ vec {f}} _ {0}: = {\ tfrac {d} {{\ vec {n}} ^ {2}}} {\ vec {n}}}$

c) I följande låt och${\ displaystyle {\ vec {n}} _ {0} = (n_ {x}, n_ {y}, n_ {z}): = {\ tfrac {\ vec {n}} {\ | {\ vec { n}} \ |}}}$

${\ displaystyle {\ vec {f}} _ {1}: = \ rho (n_ {y}, - n_ {x}, 0) / {\ sqrt {n_ {x} ^ {2} + n_ {y} ^ {2}}}}$om eller är, annars vara . (Detta alternativ garanterar ett felfritt val .)${\ displaystyle | n_ {x} |> 0,5}$${\ displaystyle | n_ {y} |> 0,5}$${\ displaystyle {\ vec {f}} _ {1}: = \ rho (0, n_ {z}, - n_ {y}) / {\ sqrt {n_ {y} ^ {2} + n_ {z} ^ {2}}}}$${\ displaystyle {\ vec {f}} _ {1}}$

För vertikal radievektor är . Så är det${\ displaystyle {\ vec {f}} _ {1}}$${\ displaystyle {\ vec {f}} _ {2}: = {\ vec {n}} _ {0} \ times {\ vec {f}} _ {1}}$

${\ displaystyle {\ vec {x}} = {\ vec {f}} _ {0} + {\ vec {f}} _ {1} \ cos t + {\ vec {f}} _ {2} \ synd t}$ en parametrisk representation av skärcirkeln.

Kontur av en sfär

Kontur: Normalt test för släta ytor

Vi vet att en sfärs riktiga konturer är en cirkel i både parallell och central projektion. Nu ska en parametrisk framställning av konturen bestämmas för en konkret projektion. Ursprungligen med parallell projektion. En skillnad behöver inte göras här mellan vinkelrät och sned parallell projektion, eftersom den verkliga konturen bara beror på projektionsriktningen.

Givet: sfär och en parallell projektion med riktning . ${\ displaystyle k: x ^ {2} + y ^ {2} + z ^ {2} = r ^ {2}, \ quad r> 0}$${\ displaystyle {\ vec {p}}}$

Önskas: Parametrisk representation av den sanna konturcirkeln.

Den sanna konturen av en slät yta skiljer synliga punkter från osynliga punkter. Huruvida en punkt är synlig eller inte kan bestämmas med hjälp av den normala vektorn (se nedan). Synliga och osynliga punkter kan nämligen kännas igen genom tecknet på den skalära produkten av ytan som är normal med projektionsriktningen. Poäng på konturen ger den skalära produkten 0. Problemet som ska lösas påminner något om ett extremt värdeproblem från skolan. Som med sökandet efter en global extremum får man inte förlita sig på de punkter som finns med konturförhållandet (se torus nedan). De kan bara vara konturpunkter lokalt. Som med det extrema värdeproblemet måste du också inkludera kanterna separat (se vas eller cylinder).

För sfären är en normal vid en punkt helt enkelt positionens vektor för den punkten. Konturförhållandena i punkten för projektionsriktningen är: ${\ displaystyle X: {\ vec {x}} = (x, y, z)}$${\ displaystyle X}$${\ displaystyle {\ vec {p}} = (a, b, c)}$

• ${\ displaystyle {\ vec {x}} \ cdot {\ vec {p}} = ax + av + cz = 0}$

Detta är ekvationen av ett plan genom sfärens centrum (= nollpunkt). Med ovanstående parametriska representation av en plan sektion av en sfär, kan både den sanna konturen (i rymden) och, efter projiceringen, den uppenbara konturen ritas. Vid projicering bör det noteras att en parallell projektion (vinkelrät eller sned) alltid representerar en linjär bild. Därför kartläggs cirkelns centrum (av den verkliga konturen) till centrum av bildcirkeln / bildellipsen och för att konjugera bildelipsens radier. ${\ displaystyle {\ vec {f}} _ {1}, {\ vec {f}} _ {2}}$

Nu ska konturen för en sfär bestämmas med central projektion:

Givet: sfär och en central projektion med ögonpunkt (projektionscentrum) . ${\ displaystyle k: x ^ {2} + y ^ {2} + z ^ {2} = r ^ {2}, \ r> 0}$${\ displaystyle O: {\ vec {z}} = (u, v, w)}$

Önskas: Parametrisk representation av den sanna konturcirkeln.

Konturvillkoren för en punkt är: ${\ displaystyle X: {\ vec {x}} = (x, y, z)}$

• ${\ displaystyle {\ vec {x}} \ cdot ({\ vec {x}} - {\ vec {z}}) = {\ vec {x}} ^ {2} - {\ vec {x}} \ cdot {\ vec {z}} = x ^ {2} + y ^ {2} + z ^ {2} -ux-vy-wz}$

${\ displaystyle = r ^ {2} -ux-vy-wz = 0}$.

Detta är ekvationen för ett plan som inte innehåller ursprunget . Övervägandena för skärningspunkten mellan en sfär och ett plan ger också en parametrisk representation av den sanna konturen i detta fall. Eftersom en central projektion inte är en linjär mappning gäller inte uttalandet om mittpunkten och konjugerad radie här. Med central projektion bör du beräkna tillräckligt många punkter av den sanna konturen och projicera dem individuellt och ansluta dem med en polygon (i bildtabellen). Projektionsformler för en central projektion finns i artikeln om central projektion.

Kontur av en paraboloid av revolution

Kontur: paraboloid med vinkelrät parallell projektion

Givet: Paraboloid och en parallell projektion med riktning . ${\ displaystyle K: z = x ^ {2} + y ^ {2}}$${\ displaystyle {\ vec {p}} = (a, b, c)}$

Önskas: konturen.

I detta fall är en normal vektor i en ytpunkt inte lika lätt att hitta som i en sfär, men om paraboloid representeras implicit av , så erhålls en normal vektor för en ytpunkt med gradienten . Konturvillkoret är här: ${\ displaystyle f (x, y, z) = x ^ {2} + y ^ {2} -z = 0}$${\ displaystyle X: {\ vec {x}} = (x, y, z)}$ ${\ displaystyle \ nabla f = (f_ {x}, f_ {y}, f_ {z}) = (2x, 2y, -1)}$

• ${\ displaystyle \ nabla f \ cdot {\ vec {p}} = (2x, 2y, -1) \ cdot (a, b, c)}$

${\ displaystyle = 2ax + 2by-c = 0}$.

Detta är ekvationen för ett vinkelrätt plan (parallellt med paraboloidaxeln). Så den verkliga konturen är en parabel (se bild).

Med hänsyn till representationen av plana sektioner av en paraboloid, som vi har gjort ovan för sfären, kan en parametrisk representation av sektionsparabolen ges (se webblänk CDKG, s. 94).

När det gäller en central projektion med en ögonpunkt (projektionscentrum) är konturens tillstånd: ${\ displaystyle O: {\ vec {z}} = (u, v, w)}$

• ${\ displaystyle \ nabla f \ cdot ({\ vec {x}} - {\ vec {z}}) = (2x, 2y, -1) \ cdot (xu, yv, zw) = 2 (x ^ {2 } + 2y ^ {2}) - z-2ux-2vy + w}$

${\ displaystyle = -2ux-2vy + z + w = ​​0}$.

Detta är ekvationen för ett plan som inte är vinkelrätt. Det vill säga den sanna konturen av paraboloid är en ellips med central projektion (ögonpunkt "utanför" paraboloid) (se webblänk CDKG, s. 98).

Kontur av en hyperboloid med ett skal av revolutionen

Kontur: einsch. Hyperboloid, vinkelrät parallell projektion

Givet: hyperboloid och en parallell projektion med riktning . ${\ displaystyle K: x ^ {2} + y ^ {2} -z ^ {2} = 1}$${\ displaystyle {\ vec {p}} = (a, b, c)}$

Önskas: konturen.

Vi använder den implicita representationen igen: ${\ displaystyle f (x, y, z) = x ^ {2} + y ^ {2} -z ^ {2} -1 = 0}$

Med är konturvillkoret: ${\ displaystyle \ nabla f = (f_ {x}, f_ {y}, f_ {z}) = (2x, 2y, -2z)}$

• ${\ displaystyle \ nabla f \ cdot {\ vec {p}} = (2x, 2y, -2z) \ cdot (a, b, c) = 2ax + 2by-2cz = 0}$.

Denna ekvation beskriver ett plan genom nollpunkten (hyperboloidens centrum). Till skillnad från sfärens konturplan är konturplanet här inte vinkelrätt mot projektionsriktningen! (se webblänk CDKG, s. 120).

När det gäller en central projektion med en ögonpunkt (projektionscentrum) är konturens tillstånd: ${\ displaystyle O: {\ vec {z}} = (u, v, w)}$

• ${\ displaystyle \ nabla f \ cdot ({\ vec {x}} - {\ vec {z}}) = (2x, 2y, -2z) \ cdot (xu, yv, zw) = 2 (x ^ {2 } + 2y ^ {2} -z ^ {2}) - 2ux-2vy-2wz}$

${\ displaystyle = -2ux-2vy + 2wz ​​+ 1 = 0}$.

Detta är ekvationen för ett plan som inte går igenom ursprunget. För en parametrisk framställning av den sanna konturen måste man här också överväga de möjliga plana sektionerna av en hyperboloid (se webblänk CDKG, s. 121).

Kontur av en torus

Kontur: torus med vinkelrät parallell projektion

En torus (ringyta) kan föreställas genom att rotera en cirkel runt en rotationsaxel som ligger i det cirkulära planet. En parametrisk representation som liknar den parametriska representationen av en sfär kan härledas från denna idé. För att erkänna att den sanna konturen inte är en plan sektion kan man använda en implicit representation (som med paraboloid och hyperboloid):

${\ displaystyle f (x, y, z) = (x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -a ^ {2}) ^ {2} -4R ^ {2} (x ^ {2} + y ^ {2}) = 0}$.

Om du beräknar konturförhållandet här kan du se att det inte är en plan ekvation . Ekvationen beskriver ett 3: e ordningens område (3: e krafter uppstår) Så du kan föreställa dig den verkliga konturen som skärningskurvan för torus med en tredje ordningens yta. Hur man beräknar enskilda punkter i denna kurva visas i weblink CDKG, s.139. ${\ displaystyle \ nabla f \ cdot {\ vec {n}} = 0}$

På bilden kan man se att det lokala konturförhållandet initialt ger punkter som täcks av andra delar av ytan. Det betyder att efter beräkning av konturpunkter baserat på konturförhållandet måste du testa för varje påstådd konturpunkt om den alls är synlig (se webblänk CDKG, s.

Kontur av en polyeder

Kontur: Normalt test för polyeder

Kontur: konvex polyeder (oktaeder, ikosaeder)

Kontur av en icke-konvex polyeder med punkter på en torus

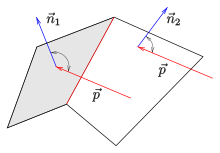
I fallet med en polyeder används det normala testet (se bild) för att testa varje (platt) delområde för att avgöra om det är synligt och sedan bestämma kanterna som hör till synliga och osynliga delområden. Dessa kanter utgör den sanna konturen. Även här måste den verkliga synligheten för icke-konvex polyeder fortfarande kontrolleras med en dold linjealgoritm (se webblänk CDKG, s. 163).

litteratur

• Fucke, Kirch, Nickel: Beskrivande geometri. Fachbuch-Verlag, Leipzig 1998, ISBN 3-446-00778-4 . S. 165
• Graf, Barner: Beskrivande geometri. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9 . S. 195
• Leopold, C.: Geometriska grunder för arkitektonisk representation. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X . S. 129

webb-länkar

• Beskrivande geometri för arkitekter (PDF; 1,5 MB). Manus (Uni Darmstadt)
• CDKG: Datorstödd beskrivande och konstruktiv geometri (TU Darmstadt) (PDF; 3,4 MB), s. 87–142