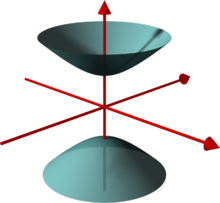
Hyperboloid

Enkel skal hyperboloid

Dubbel skal hyperboloid

I det enklaste fallet är en hyperboloid en yta som skapas genom att rotera en hyperbol runt en av dess axlar.

Under rotation av en hyperbel runt dess sidoaxel skapar en hyperboloid. Den består av en sammanhängande bit mark.
När en hyperbel roterar kring sin huvudaxel, en är dubbla skal hyperboloid skapas. Den består av två separata lappar.

Båda ytor kan beskrivas med en kvadratisk ekvation - analoga med ekvationerna av ellips och hyperbel . De är därför speciella fall av fyrkanter (t.ex. sfär , kon , paraboloid ) och skärs vanligtvis av plan i koniska sektioner .

En väsentlig skillnad mellan en enkel-skal och en dubbel-skal hyperboloid är att enkel-skal hyperboloid innehåller raka linjer , det vill säga det är en reglerad yta , två- shell hyperboloid är inte.

Denna egenskap gör single-shell hyperboloid intressant för arkitekter och civilingenjörer , eftersom hyperboloids single-shell lätt kan modelleras från raka linjer . Vissa kyltorn är i form av en hyperboloid med ett skal. Single-shell hyperboloids används också i maskinteknik för hyperboloid kugghjul, single-shell hyperboloids spelar också en roll i syntetisk geometri : Ett Minkowski-plan är geometrin för de plana sektionerna av en single-shell hyperboloid. Medan single-shell hyperboloid skärs av tangentiella plan i två korsande raka linjer (se nedan) har en dubbel-shell hyperboloid med tangentiella plan bara en punkt gemensamt och är därför geometriskt mer relaterad till en sfär .

egenskaper

Enkel-skal enhet hyperboloid

Single-shell hyperboloid: genereras genom att rotera en hyperbol (ovan) eller en rak linje (nedan: röd eller blå)

Single-shell hyperboloid: platta snitt

Om hyperbolen roteras i xz- planet runt z-axeln (se figur), erhålls hyperboloid med enkel skal med ekvationen ${\ displaystyle x ^ {2} -z ^ {2} = 1}$

${\ displaystyle H_ {1} \ colon \ x ^ {2} + y ^ {2} -z ^ {2} = 1}$ .

När rotation är ersatt med . ${\ displaystyle x ^ {2}}$ ${\ displaystyle x ^ {2} + y ^ {2}}$

Den enkla skal enhet hyperboloid resultat från att rotera den graf över den funktion kring axeln. Det gäller följande i härledningen . Den volym och ytan för en enda skalenheten hyperboloid med höjd resultat från Guldin regler med den hjälp av integraler . ${\ displaystyle f (z) = {\ sqrt {z ^ {2} +1}}}$ ${\ displaystyle z}$ ${\ displaystyle f '(z) = {\ frac {z} {\ sqrt {z ^ {2} +1}}}$ ${\ displaystyle h}$

Paraboloid av revolution med parabolor och höjdcirklar

volym

{\ displaystyle V = \ pi \ int _ {0} ^ {h} (f (z)) ^ {2} \ \ mathrm {d} z = \ pi \ int _ {0} ^ {h} z ^ { 2} +1 \ \ mathrm {d} z = \ pi \ left ({\ frac {h ^ {3}} {3}} + h \ right) = {\ frac {\ pi} {3}} \ left (h ^ {3} + 3h \ höger)}

yta

{\ displaystyle {\ begin {align} A & = 2 \ pi \ int _ {0} ^ {h} f (z) {\ sqrt {1+ \ left (f '(z) \ right) ^ {2} }} \ \ mathrm {d} z \\ & = 2 \ pi \ int _ {0} ^ {h} {\ sqrt {z ^ {2} +1}} {\ sqrt {1+ \ left ({\ frac {z} {\ sqrt {z ^ {2} +1}}} höger) ^ {2}}} \ \ mathrm {d} z \\ & = 2 \ pi \ int _ {0} ^ {h } {\ sqrt {2z ^ {2} +1}} \ \ mathrm {d} z \\ & = 2 \ pi \ left ({\ frac {1} {2}} z {\ sqrt {2z ^ {2 } +1}} + {\ frac {\ sqrt {2}} {2}} \ ln \ left ({\ sqrt {2}} z + {\ sqrt {2z ^ {2} +1}} \ right) {\ Big |} _ {z = 0} ^ {z = h} \ höger) \\ & = \ pi \ vänster (h {\ sqrt {2h ^ {2} +1}} + {\ sqrt {2} } \ ln \ vänster ({\ sqrt {2}} h + {\ sqrt {2h ^ {2} +1}} \ höger) \ höger) \ slut {justerad}}}

Parametrisk representation

Uppenbarligen är varje vertikalt snitt med ett plan en cirkel med en radie . Korsningen av planet ger de två skärningslinjerna . Genom att rotera denna raka linje får man parametriska representationer av alla raka linjer på hyperboloid: ${\ displaystyle z = z_ {0}}$ ${\ displaystyle {\ sqrt {1 + z_ {0} ^ {2}}}}$ ${\ displaystyle x = 1}$ ${\ displaystyle (1, t, \ pm t) ^ {\ top}, t \ in \ mathbb {R}}$

{\ displaystyle g _ {\ alpha} ^ {\ pm}: {\ vec {x}} (t) = {\ begin {pmatrix} \ cos \ alpha \\\ sin \ alpha \\ 0 \ end {pmatrix} } + t \ cdot {\ begin {pmatrix} - \ sin \ alpha \\\ cos \ alpha \\\ pm 1 \ end {pmatrix}} \, \ quad t \ in \ mathbb {R}, \ 0 \ leq \ alpha \ leq 2 \ pi}

Single-shell hyperboloid kan också genereras genom att rotera den raka linjen eller ( sned mot rotationsaxeln ) (se bild). Detta uttalande finns i litteraturen som uppsättning av Wren kallas. ${\ displaystyle H_ {1}}$ ${\ displaystyle g_ {0} ^ {+}}$ ${\ displaystyle g_ {0} ^ {-}}$

Tangentplan

Den ekvation av tangentplanet av en implicit givet område i en prick är . ${\ displaystyle f (x, y, z) = 0}$ ${\ displaystyle {\ vec {x}} _ {0} = (x_ {0}, y_ {0}, z_ {0})}$ ${\ displaystyle f_ {x} ({\ vec {x}} _ {0}) (x-x_ {0}) + f_ {y} ({\ vec {x}} _ {0}) (y-y_ {0}) + f_ {z} ({\ vec {x}} _ {0}) (z-z_ {0}) = 0}$

För H1 blir det resultat

${\ displaystyle x_ {0} x + y_ {0} y-z_ {0} z-1 = 0 \.}$

Planskärningar

Plan med en lutning mindre än 1 (1 är lutningen för den raka linjen på hyperboloid) skär varandra i en ellips , ${\ displaystyle H_ {1}}$
Plan med en lutning lika med 1 skär varandra genom koordinatursprunget i ett parallellt par linjer, ${\ displaystyle H_ {1}}$
Plan med en lutning lika med 1 skär inte genom ursprunget i en parabel , ${\ displaystyle H_ {1}}$
Tangentiella plan skär varandra i ett korsande parpar, ${\ displaystyle H_ {1}}$
Plan med en lutning större än 1 som inte är tangentplan skär varandra i en hyperbol . ${\ displaystyle H_ {1}}$

Ett plan som innehåller en hyperboloid rak linje är antingen ett tangentiellt plan och innehåller således en andra skärande hyperboloid rak linje eller innehåller en hyperboloid rak linje som är för parallell och är därför ett tangentiellt plan vid en avlägsen punkt. ${\ displaystyle e}$ ${\ displaystyle e}$ ${\ displaystyle e}$

Avgränsa bilder

Analogt med hur varje ellips kan förstås som en affin bild av enhetscirkeln , vilken som helst är enkla skal hyperboloid den affina bilden av enheten hyperboloid . De enklaste affina bilderna erhålls genom att skala koordinataxlarna: ${\ displaystyle H_ {1}}$

${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} - {\ frac {z ^ {2} } {c ^ {2}}} = 1 \, \ a, b, c> 0.}$

I fallet är de vertikala sektionerna cirklar . Annars är de ellipser . En sådan hyperboloid kallas en rotationshyperboloid med ett skal . Det faktum att varje hyperboloid med en skal alltid innehåller cirklar visas i det cirkulära sektionsplanet. ${\ displaystyle a = b}$

Eftersom hyperboloid med enkel skal innehåller raka linjer är det en reglerad yta . Eftersom varje tangentplanet till ett enkelskal hyperboloid skär den yta nära dess kontaktpunkt , den har en negativ Gaussisk krökning och kan därför inte tas fram, i motsats till de regelytor koner och cylindrar , som har Gausskrökningen 0. Följande parametriska representation av hyperboloid erhålls från den vanliga parametriska representationen av en hyperbol med hyperboliska funktioner ${\ displaystyle {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^ {2}} {b ^ {2}}} - {\ tfrac {z ^ {2} } {c ^ {2}}} = 1:}$

{\ displaystyle {\ vec {x}} (s, t) = \ left ({\ begin {array} {lll} a \ cosh s \ cos t \\ b \ cosh s \ sin t \\ c \ sinh s \ end {array}} \ right), \ quad s \ in \ mathbb {R}, \ 0 \ leq t \ leq 2 \ pi}

Homogena koordinater

Om man introducerar homogena koordinater på ett sådant sätt att fjärrplanet beskrivs av ekvationen , måste man ställa in. Efter eliminering av nämnaren erhålls den homogena beskrivningen av ekvationen: ${\ displaystyle x_ {4} = 0}$ ${\ displaystyle x = {\ tfrac {x_ {1}} {x_ {4}}}, y = {\ tfrac {x_ {2}} {x_ {4}}}, z = {\ tfrac {x_ {3 }} {x_ {4}}}}$ ${\ displaystyle H_ {1}}$

{\ displaystyle x_ {1} ^ {2} + x_ {2} ^ {2} -x_ {3} ^ {2} -x_ {4} ^ {2} = 0}

.

Korsningen av hyperboloid med det bortre planet är en cirkel . Omvandlingen till och efterföljande introduktion av nya koordinater ger beskrivningen av hyperboloid med enkel skal i homogena koordinater genom ekvationen ${\ displaystyle x_ {4} = 0}$
${\ displaystyle (x_ {1} -x_ {3}) (x_ {1} + x_ {3}) + (x_ {2} -x_ {4}) (x_ {2} + x_ {4}) = 0 }$ ${\ displaystyle u_ {1} = x_ {1} -x_ {2}, \; u_ {2} = x_ {1} + x_ {3}, \; u_ {3} = x_ {2} -x_ {4 }, \; u_ {4} = x_ {2} + x_ {4} \;}$

{\ displaystyle u_ {1} u_ {2} + u_ {3} u_ {4} = 0 \.}

I de nya koordinaterna skär planet hyperboloid i två raka linjer . Om man introducerar affinakoordinater igenom , får man ekvationen av en hyperbol paraboloid : ${\ displaystyle u_ {4} = 0}$
${\ displaystyle x = {\ tfrac {u_ {1}} {u_ {4}}}, y = {\ tfrac {u_ {2}} {u_ {4}}}, z = {\ tfrac {u_ {3 }} {u_ {4}}}}$

{\ displaystyle z = -xy \.}

Detta visar: En enkelskalig hyperboloid motsvarar projektivt en hyperbolisk paraboloid .

Dubbel skal hyperboloid

Tvåskalig hyperboloid

Double-shell hyperboloid: genereras genom att rotera en hyperbol

Dubbelskalig hyperboloid: planskärning

Om hyperbolen roteras runt z-axeln i xz- planet (se bild ), erhålls tvåskalsenheten hyperboloid med ekvationen eller i den vanliga formen ${\ displaystyle -x ^ {2} + z ^ {2} = 1}$ ${\ displaystyle -x ^ {2} -y ^ {2} + z ^ {2} = 1}$

${\ displaystyle H_ {2} \ colon \ x ^ {2} + y ^ {2} -z ^ {2} = - 1}$ .

Korsningen av planet med är en cirkel (om ) eller en punkt (om ) eller tom (om ). består av två delar, motsvarande de två delarna av hyperbolen . ${\ displaystyle z = z_ {0}}$ ${\ displaystyle H_ {2}}$ ${\ displaystyle z_ {0} ^ {2}> 1}$ ${\ displaystyle z_ {0} = \ pm 1}$ ${\ displaystyle z_ {0} ^ {2} <1}$ ${\ displaystyle H_ {2}}$

Två-skalenheten hyperboloid resultat från att rotera den graf över den funktion kring axeln. Det gäller följande i härledningen . Den volym och ytan för en två-shell enhet hyperboloid med höjd resultat från Guldin regler med den hjälp av integraler . ${\ displaystyle f (z) = {\ sqrt {z ^ {2} -1}}}$ ${\ displaystyle z}$ ${\ displaystyle f '(z) = {\ frac {z} {\ sqrt {z ^ {2} -1}}}$ ${\ displaystyle h-1}$