Hyperbolisk geometri

Modell av en tegelplatta av ett plan med fyrkanter. Mer än fyra möts i hörnen (beroende på storlek, här fem).

Den hyperboliska geometrin (även kallad Lobachevskian geometry eller Lobachevsky geometry ) är ett exempel på en icke-euklidisk geometri som erhålls om man lägger till den motsägelsefulla hyperboliska axiomen till axiomerna för absolut geometri istället för axiomet av paralleller som kännetecknar de euklidiska geometrierna . Detta betyder att för en rak linje g och en punkt P (som inte ligger på g ) finns det inte bara en, som i euklidisk geometri, utan minst två raka linjer ( h och i ) som går genom P och är parallella med g . Det faktum att två raka linjer är "parallella" med varandra betyder bara att de ligger i samma plan och har inga punkter gemensamt, inte att de har samma avstånd överallt ( h och jag har bara en punkt P gemensamt ).

Det kan visas att för alla raka linjer g genom vilken punkt som helst utanför g finns det oändligt många icke- skärande linjer ("paralleller") som ligger i det plan som definieras av punkten och linjen. Två av dem är i ett gränsfall position och kallas border- parallellt (även: horoparallel) till den räta linjen, medan de återstående raka linjer kallas superparallel (även: hyperparallel).

Representationer av det verkliga hyperboliska planet

Det finns olika sätt på vilka det verkliga hyperboliska planet kan representeras i det verkliga euklidiska planet. De flesta av dessa kan generaliseras till högre dimensioner.

På vart och ett av dessa sätt representeras samma abstrakta hyperboliska geometri: det verkliga hyperboliska planet. Det är därför möjligt att konvertera mellan dessa representationer och uttalanden i rent hyperbolisk geometri är oberoende av den "använda" modellen. Vanligtvis talar man om olika modeller i matematik när två icke-isomorfa strukturer uppfyller samma axiomsystem. I detta avseende beskriver följande "modeller" samma struktur, så de är bara olika representationer av en modell. Men dessa framställningar kallas alltid modeller i litteraturen , inklusive här. För hyperboliska plan över andra kroppar och mer än tvådimensionella hyperboliska utrymmen, se Metrisk absolut geometri .

Cirkulär skivmodell från Beltrami och Klein

I denna framställning utvecklad av Eugenio Beltrami och Felix Klein gäller följande:

• Det hyperboliska planet modelleras av en öppen cirkulär skiva.
• Hyperboliska linjer modelleras av senor .
• Längder definieras av en speciell avståndsfunktion (vinklarna skiljer sig också från de euklidiska värdena).

Denna framställning är också känd under namnet "ölmatta-geometri".

Avståndsfunktion

Avstånd mellan två punkter i en hyperbolisk geometri

Är A och B , två punkter av den cirkulära skivan, så att genom möter A och B som sträcker sig ackord cirkeln i två punkter R och S . Det hyperboliska avståndet mellan A och B definieras nu med det dubbla förhållandet: ${\ displaystyle (A, B, R, S)}$

${\ displaystyle d (A, B) = {\ frac {1} {2}} \ ln (A, B, R, S) = {\ frac {1} {2}} \ ln {\ frac {{\ overline {RB}} \ cdot {\ overline {SA}}} {{\ overline {RA}} \ cdot {\ overline {SB}}}}}$.

Poincaré cirkulär skivmodell

Följande gäller den cirkulära skivmodellen av Henri Poincaré , som går tillbaka till Beltrami :

• Det hyperboliska planet modelleras av en öppen cirkulär skiva (vanligtvis enhetscirkeln).
• Hyperboliska raka linjer modelleras av bågar (och diametrar ) som är vinkelräta mot kanten.
• Den hyperboliska vinkelmätningen motsvarar den euklidiska vinkelmätningen, vinkeln mellan två bågar bestäms av deras tangenter vid skärningspunkten.
• Den hyperboliska längdmätningen utförs med en speciell avståndsfunktion.

Avståndsfunktion

Låt och vara två punkter på den cirkulära skivan. Summera planet som komplexa planet, så motsvarar de punkter , komplexa tal , . Det hyperboliska avståndet från och definieras nu med hjälp av dessa komplexa tal: ${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle A}$${\ displaystyle B}$

${\ displaystyle d (A, B) = \ operatorname {arcosh} \ left (1 + {\ frac {2 \ cdot \ left \ | ab \ right \ | ^ {2}} {\ left (1- \ left \ | a \ höger \ | ^ {2} \ höger) \ cdot \ vänster (1- \ vänster \ | b \ höger \ | ^ {2} \ höger)}} höger)}$

Poincaré halvplanmodell

I Henri Poincarés halvplanmodell, som går tillbaka till Beltrami:

• Det hyperboliska planet modelleras av det övre halva planet (y> 0).
• Hyperboliska raka linjer modelleras av bågar (och halvlinjer ) som är vinkelräta mot x-axeln.
• Den hyperboliska vinkelmätningen motsvarar den euklidiska vinkelmätningen, varvid vinkeln mellan två cirkelbågar bestäms via deras tangenter vid skärningspunkten.

Avståndsfunktion

Avståndet mellan två punkter i det övre halvplanet beräknas med följande formel:

${\ displaystyle \ operatorname {d} (\ langle x_ {1}, y_ {1} \ rangle, \ langle x_ {2}, y_ {2} \ rangle) = \ operatorname {arcosh} \ left (1 + {\ frac {{(x_ {2} -x_ {1})} ^ {2} + {(y_ {2} -y_ {1})} ^ {2}} {2y_ {1} y_ {2}}} \ rätt) \ ,.}$

Hyperboloid modell

Hyperboloidmodellen, som går tillbaka till Poincaré, bäddar in det hyperboliska planet i det tredimensionella Minkowski-utrymmet .

Erlangen-programmet

I betydelsen av Felix Kleins Erlanger-program är hyperbolisk geometri geometrin av

${\ displaystyle (O (n, 1), O (n) \ times O (1))}$.

Beltrami-Klein-modellen visar att hyperbolisk geometri kan förstås som en del av projektiv geometri.

triangel

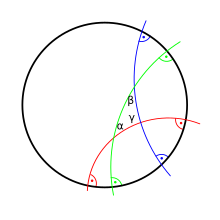
Triangel i hyperboliskt utrymme

I verklig hyperbolisk geometri är summan av vinklarna i en triangel alltid mindre än π (180 grader; eller två rättigheter, om du vill undvika vinkelmåttet). För mycket stora trianglar kan den göras så liten som du vill. Triangelns yta beräknas med hjälp av Johann Heinrich Lamberts formel:

${\ displaystyle \ pi - (\ alpha + \ beta + \ gamma) = C \, \ Delta,}$

där α , β och γ är respektive vinklar, Δ är arean och konstanten C är en skalningsfaktor. Skalningsfaktorn C beror på systemet för enheter som används och bör i grunden ställas in på 1. Om faktorn C är negativ, talar man om en (positiv) Gaussisk krökning . På samma sätt definierade Thomas Harriot tidigare formeln 1603

${\ displaystyle \ Delta = R ^ {2} \, (\ alpha + \ beta + \ gamma - \ pi)}$

för området av en triangel på en sfärisk yta som bildas av cirklar med samma radie som sfären. Förhållandet gäller här

${\ displaystyle C = - {\ frac {1} {R ^ {2}}}}$.

Eftersom den hyperboliska geometrin kräver ett positivt värde för C , måste R bero på

${\ displaystyle R = (- C) ^ {- {\ frac {1} {2}}}}$

agera runt en imaginär radie.

Se även

• Hyperboliskt utrymme
• Elliptisk geometri
• Nikolai Lobachevsky
• János Bolyai
• Giovanni Girolamo Saccheri och Saccheri-Viereck

litteratur

historia

• Jeremy Gray: Idéer om rymden: euklidisk, icke-euklidisk och relativistisk . 2: a upplagan. Oxford University Press, Oxford 1989, ISBN 0-19-853935-5 . 
• Marvin Jay Greenberg: Euklidiska och icke-euklidiska geometrier: utveckling och historia. WH Freeman, 1993, ISBN 0-7167-2446-4 .
• David Hilbert : Fundamentals of Geometry . 14: e upplagan. Teubner, Stuttgart / Leipzig 1999, ISBN 3-519-00237-X ( online-kopia av 1903-upplagan [nås 28 juni 2013]). 
• Nikolai I. Lobachevsky: Pangeometry, redigerad och översatt av Athanase Papadopoulos, Heritage of European Mathematics. Vol. 4, European Mathematical Society (EMS), Zürich, ISBN 978-3-03719-087-6 .

Den hyperboliska geometrin i samband med differentiell geometri (geometrier på ytor)

• Norbert A'Campo, Athanase Papadopoulos: Anteckningar om hyperbolisk geometri. I: Strasbourg Master Class om geometri. European Mathematical Society (EMS), Zürich, ISBN 978-3-03719-105-7 , s. 1–182, doi: 10.4171 / 105 . (IRMA-föreläsningar i matematik och teoretisk fysik, Vol. 18)
• Athanase Papadopoulos (red.): Handbok om Teichmüllers teori. Vol. I, European Mathematical Society (EMS), Zürich 2007, ISBN 978-3-03719-029-6 , doi: 10.4171 / 029 . (IRMA-föreläsningar i matematik och teoretisk fysik 11)
• Athanase Papadopoulos (red.): Handbok om Teichmüllers teori. Vol. II, European Mathematical Society (EMS), Zürich 2009, ISBN 978-3-03719-055-5 , doi: 10.4171 / 055 . (IRMA-föreläsningar i matematik och teoretisk fysik 13)
• Athanase Papadopoulos (red.): Handbok om Teichmüller-teorin. Vol. III, European Mathematical Society (EMS), Zürich 2012, ISBN 978-3-03719-103-3 , doi: 10.4171 / 103 . (IRMA-föreläsningar i matematik och teoretisk fysik 19)

Det (verkliga) hyperboliska planet som en modell för en absolut geometri i Hilbertiansk mening

• Friedrich Bachmann : Geometriens struktur utifrån begreppet reflektion . 2: a kompletterad utgåva. Springer, Berlin / Heidelberg / New York 1973, ISBN 3-540-06136-3 , V: Hyperbolisk geometri och §20.13: Hilbert Planes ( definierar absolut geometri mycket allmänt, förklarar de speciella egenskaperna hos verklig hyperbolisk geometri mot denna bakgrund). 
• Benno Klotzek: Euklidiska och icke-euklidiska elementära geometrier . 1: a upplagan. Harri Deutsch, Frankfurt am Main 2001, ISBN 3-8171-1583-0 ( elementärt betyder inte bara här : lösa bygguppgifter och samordna de "klassiska" icke-euklidiska geometrierna). 

Individuella bevis

1. ↑ ^{a b} Klotzek (2001), 2.1
2. ↑ Susanne Müller-Philipp, Hans-Joachim Gorski: Guide till geometri: För studenter på lärarplatser . Vieweg + Teubner Verlag, 5: e utökade upplagan, 2012, ISBN 978-3-8348-1234-6 , s 71 ( utdrag (Google) )